Nữ tiến sĩ 9x giải thành công bài toán đỉnh cao của thế kỷ 21: Một huy chương "Nobel Toán học" đang chờ cô ấy vào năm 2026

Vương Hồng, một nhà toán học sinh năm 1991 người Trung Quốc, vừa giải thành công "Giả thuyết Kakeya" cho không gian 3 chiều, một bài toán đã tồn tại hơn 100 năm và được đánh giá là đỉnh cao của thế kỷ 21.

"Đó chắc chắn sẽ là một trong những thành tựu toán học hàng đầu trong thế kỷ này", Eyal Lubetzky, một nhà toán học tại Đại học New York cho biết.

Có cùng nhận định với ông là giáo sư Terence Chi-Shen Tao, nhà toán học gốc Hoa được mệnh danh là "Mozart toán học", người từng nhận Huy chương Fields năm 2006 nhưng cũng thất bại trong việc giải "Giả thuyết Kakeya" cho không gian 3 chiều.

"Tôi rất vui mừng thông báo rằng Giả thuyết Kakeya, một trong những bài toán mở được tìm kiếm nhiều nhất trong lý thuyết đo lường hình học, hiện đã được Vương Hồng và Joshua Zahl chứng minh", giáo sư Tao cho biết.

Việc chứng minh được Giả thuyết Kakeya trong không gian 3 chiều hứa hẹn sẽ mở đường cho nhiều hướng nghiên cứu mới trong các lĩnh vực giải tích điều hòa, lý thuyết số và toán tổ hợp. Bước đột phá này có thể tác động đến các ứng dụng trong khoa học máy tính như tạo sinh hình ảnh, xử lý dữ liệu và truyền thông không dây.

Với thành tựu ấy, Vương Hồng hiện được đánh giá là một ứng cử viên sáng giá cho Huy chương Fields - giải thưởng danh giá nhất lĩnh vực được mệnh danh là "Nobel Toán học" –sẽ được trao vào năm 2026.

Bắt đầu từ bài toán về một cây kim

Giả thuyết Kakeya bắt nguồn từ một bài toán được đặt ra bởi nhà toán học người Nhật Soichi Kakeya vào năm 1917. Thoạt nghe, nó chẳng khác gì một bài tập hình học vui dành cho học sinh trung học:

Giả sử, bạn có một cây kim đặt trên một mặt phẳng. Bây giờ, bạn cần tìm ra một cách để xoay cây kim đó, sao cho đầu của nó chỉ theo đủ mọi hướng, đồng thời, diện tích mà nó quét trên mặt phẳng là nhỏ nhất.

Thông thường, tất cả chúng ta sẽ đều bắt đầu bằng việc thử xoay cây kim đó theo hình vòng tròn. Lúc này, cây kim sẽ quét qua một diện tích bằng chính hình tròn có đường kính bằng độ dài của nó.

Nhưng Soichi Kakeya đã đưa ra một lời giải thông minh hơn, rằng ông có thể xoay cây kim đủ 360 độ, quét qua một hình tam giác lõm chỉ có diện tích bằng một nửa so với hình tròn ban đầu:

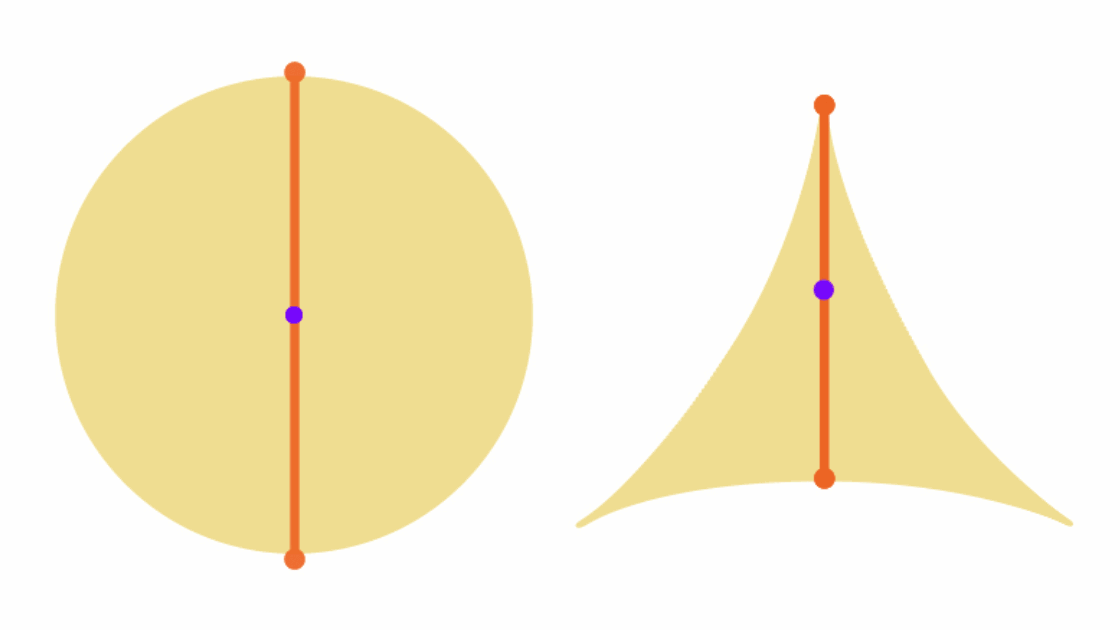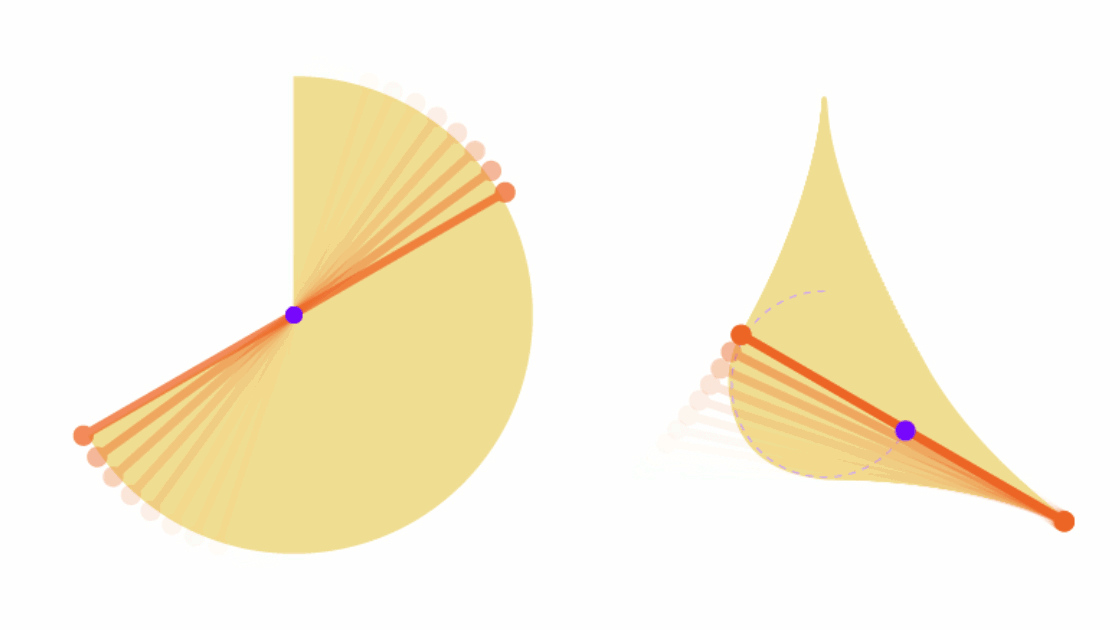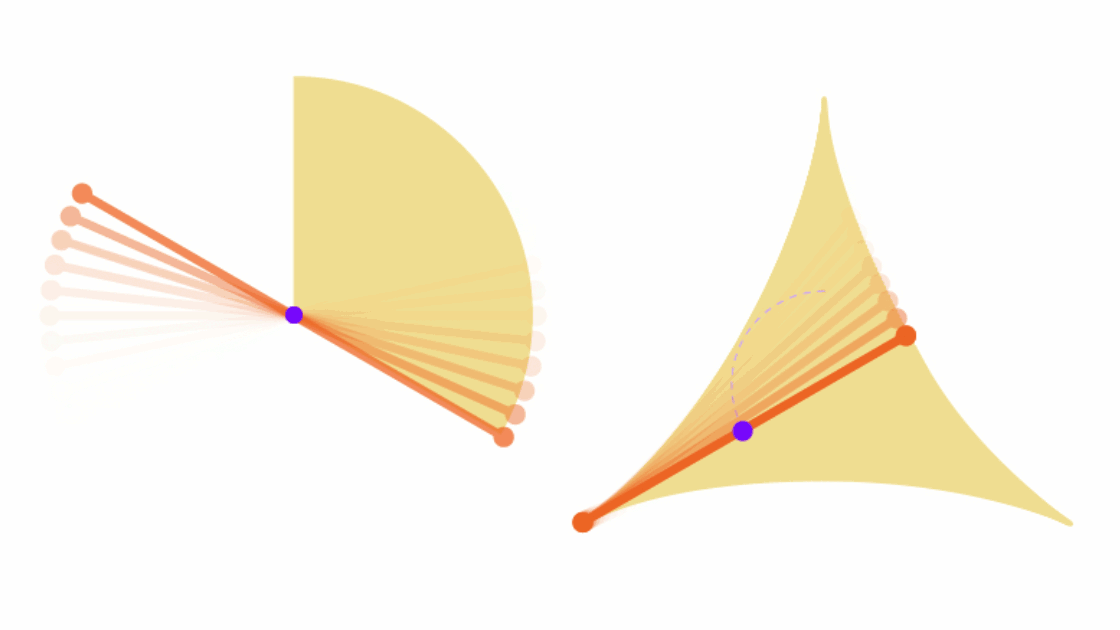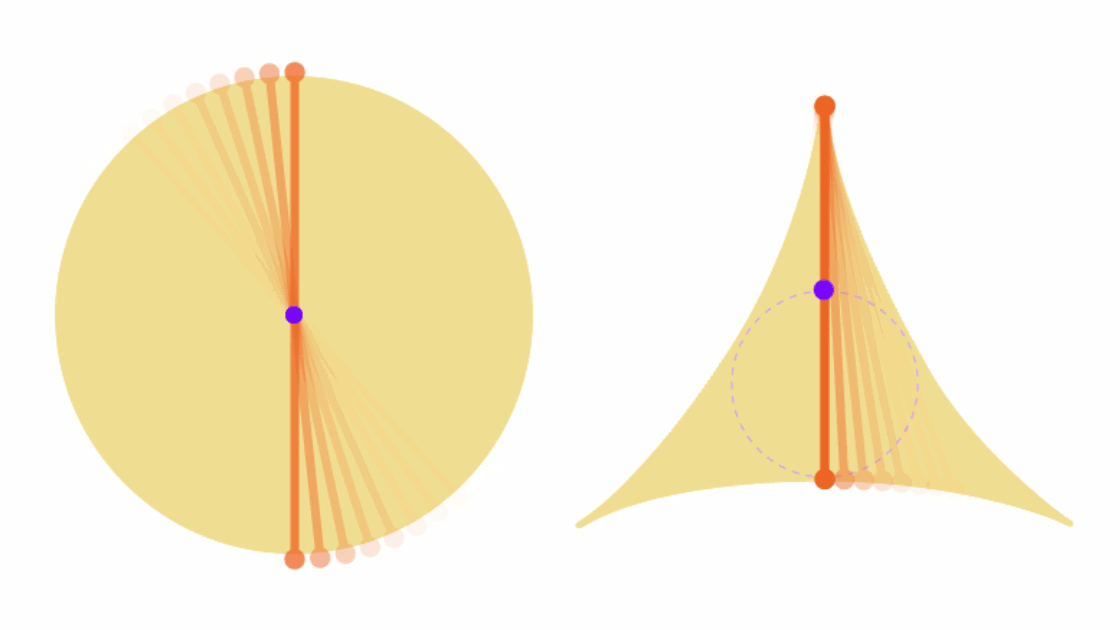
Lời giải này sau đó chỉ tồn tại được 2 năm. Bởi Abram Besicovitch, một nhà toán học người Nga đã chứng minh được rằng nếu cây kim có độ dày siêu mỏng, xấp xỉ bằng 0, thì ông có thể xoay nó đủ mọi hướng và quét qua một diện tích cũng xấp xỉ bằng 0.

Lời giải của Besicovitch được đưa ra vào năm 1919, nhưng do Chiến tranh thế giới thứ nhất và Cách mạng Nga, kết quả của nó phải mất vài năm mới được công bố với phần còn lại của thế giới.

Nghe có vẻ rất mơ hồ, tại sao bạn có thể xoay một cây kim 360 độ và quét qua một diện tích bằng 0?

Để hiểu lời giải của Besicovitch, bạn hãy hình dung mình đang cầm trên tay một lá bài. Nhiệm vụ của bạn là phải cắt đôi lá bài này theo chiều dày của nó, để có được 2 lá bài mỏng bằng một nửa lá bài cũ.

Sau đó, bạn xòe chúng ra một chút, chỉ một chút để hai lá bài chồng lên nhau nhiều nhất có thể. Tiếp đó, bạn lại cắt đôi hai lá bài này để được 4 lá, rồi 8 lá… tiếp tục xòe chúng ra chỉ một chút.

Cuối cùng, nếu bạn cắt những lá bài vô hạn lần và xòe chúng ra vô hạn, về lý thuyết, bạn sẽ có được một khoảng không gian đủ cho cây kim xoay 360 độ, nhưng diện tích của lá bài sẽ biến mất, trở về con số 0.

Đây rõ ràng là một nghịch lý, nhưng có thể được chứng minh bằng toán học. Và sự thật là nó đã được chứng minh từ cách đây hơn 100 năm, bởi nhà toán học người Nga Abram Besicovitch.

Mở rộng lên không gian n chiều

Về cơ bản, Abram Besicovitch đã giải được hoàn toàn câu hỏi ban đầu mà Soichi Kakeya đã đặt ra, và lẽ ra bài toán nên kết thúc ở đó. Tuy nhiên, vài thập kỷ sau, các nhà toán học bắt đầu nghiên cứu một khía cạnh khác của bài toán Kakeya ban đầu.

Họ tự hỏi: Sau khi cây kim đã xoay đủ theo các hướng, tập hợp của không gian mà nó chiếm chỗ sẽ có chiều bằng bao nhiêu?

Trong toán học, chiều là một thước đo độ phức tạp. Nó thường được định nghĩa là số lượng hướng mà bạn có thể di chuyển trong không gian đó. Ví dụ, một điểm sẽ có chiều bằng 0. Vì nó chỉ là một chấm không dài, không rộng và không cao.

Một đường thẳng có 1 chiều, vì bạn chỉ có thể di chuyển tới lui trên nó như đi trên một sợi dây. Ngược lại, một mặt phẳng như tờ giấy sẽ có 2 chiều ngang, dọc. Và không gian 3 chiều như chúng ta đang sống ở đây, trong một tòa nhà có thể đi lại trên mặt đất theo 2 chiều, cộng thêm một chiều cao khi đi lên và đi xuống tầng hầm.

Nhưng toán học không dừng lại ở đó. Có những thứ kỳ lạ hơn, như hình phân dạng fractal đã được chứng minh có thể có chiều thập phân, ví dụ 1,5 chiều. Điều này có nghĩa là chúng nằm đâu đó "nửa vời" giữa các chiều, vừa phức tạp hơn đường thẳng nhưng chưa đủ để trở thành mặt phẳng.

Biết được chiều của một đối tượng trong toán học đồng nghĩa với việc nắm được độ phức tạp cơ bản của đại lượng đó, vì các nhà toán học sẽ biết được mức độ "tự do" di chuyển của đối tượng đó.

Vì vậy, họ cũng cần biết được một chiếc kim sẽ xoay được bao nhiêu chiều trong bài toán của Kakeya.

Năm 1971, Roy Davies, một nhà toán học người Anh đã chứng minh được khi bạn xoay một chiếc kim trên mặt phẳng 2D, số chiều mà không gian xoay hay tập hợp Kakeya tạo ra luôn là 2, ngay cả khi diện tích của nó bằng 0, như một điểm trên không gian 0 chiều.

Nhưng trong toán, các nhà toán học rất thích khái quát hóa. Họ muốn kiểm tra bài toán Kakeya trong tất cả các không gian bất kỳ có n chiều. Liệu một cây kim quay theo tất cả n hướng có luôn bao phủ một thể tích n chiều?

Phỏng đoán này chính là Giả thuyết Kakeya, và trong suốt 100 năm, chưa ai có thể chứng minh được nó.

Nữ toán học gia 9x người Trung Quốc ghi tên vào lịch sử khi chứng minh được Giả thuyết Kakeya cho không gian 3 chiều

Một trong những bước đầu tiên và quan trọng nhất để chứng minh Giả thuyết Kakeya tổng quát là phải chứng minh được nó đúng với không gian 3 chiều. Một cây kim xoay mọi hướng trong không gian 3 chiều cũng phải tạo thành một tập hợp 3 chiều.

Nghe thì tưởng chừng rất hiển nhiên và đơn giản, nhưng bài toán này đã đánh bại hàng loạt thế hệ nhà khoa học thông thái nhất hành tinh, những người từng muốn giải quyết nó trong hàng thập kỷ.

Vào năm 1995, Thomas Wolff, một nhà toán học người Mỹ đã chứng minh được chiều của tập hợp Kakeya trong không gian 3 chiều phải lớn hơn 2,5.

Đến năm 1999, nhà toán học người Úc gốc Hoa Terence Chi-Shen Tao đã đạt được một bước tiến được coi là đột phá, khi ông có thể nâng số chiều chứng minh được của tập Kakeya lên lớn hơn 2,500000001 chiều.

Chênh lệch 0,000000001 đó đủ để giáo sư Tao xuất bản một bài báo trên tạp chí toán học uy tín hàng đầu thế giới Annals Mathematics.

Vậy để thấy, những gì mà Vương Hồng, nữ nhà toán học 9x người Trung Quốc đã làm được đột phá thế nào khi bây giờ, cô đã chứng minh được số chiều của tập Kakeya trong không gian 3 chiều bằng đúng 3.

Sinh năm 1991 tại Quế Lâm, Trung Quốc, Vương Hồng được coi là một trong những thần đồng toán học của quốc gia này vào đầu thập niên 2000. Ở bậc tiểu học, cô đã nhảy một lúc 3 lớp nhờ khả năng học nhanh của mình.

Năm 16 tuổi, Vương Hồng đã đỗ đại học với điểm số 653/750, giành suất vào Trường Khoa học Trái đất và Không gian của Đại học Bắc Kinh – một trong những trường danh giá nhất Trung Quốc.

Sau một năm học tập, cô chuyển sang Khoa Toán học của trường này và tốt nghiệp cử nhân toán vào năm 2011. Vương Hồng sau đó sang Pháp làm thạc sĩ và tiếp tục tới Mỹ lấy bằng tiến sĩ toán học tại Viện Công nghệ Massachusetts (MIT) vào năm 2019.

Đây cũng là khoảng thời gian mà Vương Hồng bắt đầu theo đuổi Giả thuyết Kakeya. Hướng đi mà cô chọn về cơ bản giống với giáo sư Terence Chi-Shen Tao. Để chứng minh tập hợp Kakeya có số chiều bằng 3 trong không gian 3 chiều, cả Tao và Vương Hồng đã đều đưa ra một giả định rằng số chiều của nó bé hơn 3 và chứng minh điều đó là không thể.

Đây được gọi là phương pháp phản mệnh đề. Tao đã không thể phủ nhận phản mệnh đó, nhưng Vương Hồng, bằng cách sử dụng một kỹ thuật gọi là lý thuyết chiếu bây giờ đã có thể làm được. Cô đã chứng minh nếu một cây kim xoay mọi hướng trong không gian 3 chiều, mà tập hợp Kakeya của nó có chiều nhỏ hơn 3, thì cây kim không thể tồn tại.

"Đây là sự ủng hộ mạnh mẽ cho tính đúng đắn của giả thuyết Kakeya", Pablo Shmerkin, một nhà toán học tại Đại học British Columbia nhận xét. Mặc dù hiện nó mới chỉ đúng cho không gian 3 chiều, nhưng kỹ thuật của Vương Hồng có thể tiếp tục được sử dụng để chứng minh Giả thuyết Kakeya ở các chiều cao hơn.

Điều này có ý nghĩa cực kỳ quan trọng, hãy tưởng tượng thay vì xoay một cây kim để nó chiếm ít chỗ nhất trong một không gian, bài toán ứng dụng của chúng ta là xoay một hạt vật chất, xoay sóng âm hoặc sóng điện từ, sao cho chúng tiết kiệm năng lượng nhất.

Giả thuyết Kakeya được chứng minh sẽ mở ra một loạt ứng dụng mới không chỉ trong toán học, mà còn cả các lĩnh vực khoa học tự nhiên như vật lý và hóa học. Với thành tựu này, Vương Hồng được cho là sẽ trở thành một ứng cử viên nặng ký của Giải thưởng Fields vốn được mệnh danh là "Nobel Toán học".

Nếu điều đó trở thành sự thật, Vương Hồng sẽ là người Trung Quốc đầu tiên nhận giải thưởng danh giá này. Dù Trung Quốc là một quốc gia có nền toán học phát triển mạnh, đặc biệt khi học sinh của họ thường nhận giải thưởng lớn trong các cuộc thi quốc tế như Olympic Toán học (IMO), chưa từng có nhà toán học Trung Quốc lớn lên ở đại lục nào đoạt giải Fields.

Trong lịch sử chỉ có 2 người gốc Hoa là Shing-Tung Yau (quốc tịch Mỹ) và Terence Tao (quốc tịch Úc) giành giải thưởng này. Việt Nam cũng có một người giành được giải thưởng Fields, đó là giáo sư Ngô Bảo Châu vào năm 2010.

Khác với các giải thưởng Nobel được trao hàng năm, Huy chương Fields chỉ được trao 4 năm một lần. Lần gần nhất giải thưởng này được trao là năm 2022, vì vậy, Vương Hồng sẽ có thể bắt đầu tranh giải thưởng này từ năm 2026.