Đừng tưởng giỏi toán nhất lớp đã là siêu nhé!
Hãy cùng chiêm ngưỡng những con người của toán học dưới đây cũng như những công trình nghiên cứu xuất sắc của họ nhé:
1. Một người giao hàng ở Trung Quốc tìm ra cách giải cực kì đơn giản cho bài toán vô cùng phức tạp.
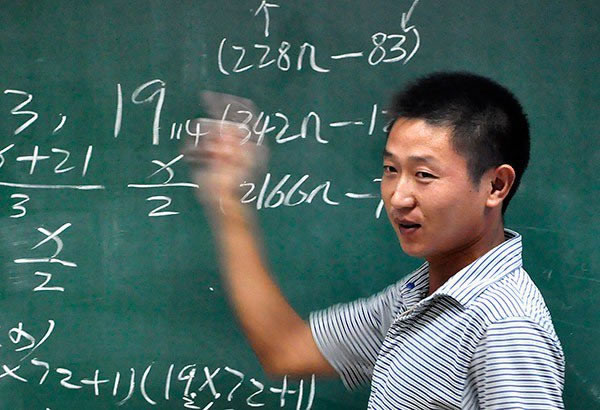
Yu Jianchun, một công nhân nhập cư Trung Quốc từ tỉnh Hà Nam, không có đào tạo toán học và không có bằng đại học nhưng đang được ca ngợi như là một phiên bản thực tế của Will Hunting, nhân vật do Matt Damon thủ vai trong Good Will Hunting – bộ phim đạt giải Oscar năm 1997, sau khi tìm thấy một phương pháp khác để xác minh số Carmichael.
Số Carmichael, còn được gọi là "số giả nguyên tố," là một số nguyên tố xác suất (tiếng Anh: probable prime ) nhưng không phải là số nguyên tố.. Chúng được sử dụng để mã hóa thẻ tín dụng và thanh toán trực tuyến, và được ứng dụng ở nhiều ứng dụng khác. Một số phương pháp đã được thực hiện để tìm ra các số nguyên tố và các số Carmichael, nhưng việc tìm ra những con số đó quả thực là một vấn đề nan giải. Tuy vậy, Yu đã đưa ra một cách đơn giản hơn nhiều để xác minh số Carmichael.
Yu cho biết ông đã tìm giải pháp trong suốt tám năm qua, chỉ dựa vào trực giác của mình và khả năng cảm nhận bẩm sinh của mình với các con số. Ông đã làm tất cả khi có thời gian rảnh vì công việc chính của ông là một người giao hàng cho một công ty logistics.
Sau khi xác minh giải pháp của mình về số Carmichael, Yu dường như đã gửi nghiên cứu của mình cho nhiều trường đại học, nhưng các trường hầu như không quan tâm và cho rằng ông chỉ là một người giao hàng không có kiến thức chuyên sâu nghiên cứu trong toán học. Nhưng mới đây, ông đã có cơ hội để trình bày nghiên cứu của mình tại Đại học Chiết Giang, cùng với các giải pháp cho bốn vấn đề toán học phức tạp khác. Cách xác minh số Carmichael của Yu đã làm những người tham dự khác sững sờ, trong đó có Giáo sư Cai Tianxin, ông cho rằng phương pháp Yu hiệu quả hơn nhiều so với các giải pháp truyền thống.
2. Giáo sư người Nigeria giải được vấn đề làm đau đầu các nhà toán học suốt 156 năm qua

Một giáo sư người Nigeria có tên Opeyemi Enoch được cho là đã giải quyết được một vấn đề toán học có tuổi đời lên đến 165 năm. Vị giáo sư giảng dạy tại Đại học Liên bang tại thành phố Oye Ekiti này có thể nhận được giải thưởng lên đến 1 triệu USD (657,000 bảng Anh) nếu công thức của mình là đúng.
Trước khi bạn đi suy nghĩ rằng đây là một cách nhanh chóng để trở nên giàu có, bạn cần phải hiểu chính xác những gì Enoch (có thể) thực hiện. Ông tin rằng ông đã tìm thấy một giải pháp cho giả thuyết Riemann - một vấn đề toán học được nhà toán học người Đức Bernhard Riemann đề xuất vào năm 1859. Nó là một trong bảy "vấn đề thiên niên kỷ" - tập hợp các câu hỏi của Viện nghiên cứu toán Clay đề xuất vào năm 2000.
3. Người phụ nữ giải được vấn đề toán học bỏ ngỏ trong suốt 7 thập kỉ

Neena Gupta là một thiên tài và đã cô đã tạo ra một kỳ công đáng ghi nhận. Trong năm 2014, cô được nhận Huân chương cho nhà khoa học trẻ của Học viện Khoa học Quốc gia Ấn Độ (INSA) vì đã giải quyết được một vấn đề toán học, mà đáng ngạc nhiên, vẫn bị bỏ ngỏ trong gần 70 năm!
Vấn đề mà không có ai ngoài Neena có thể giải quyết được gọi là Zariski Cancellation Conjecture (Gỉa thuyết huỷ bỏ Zariski). INSA mô tả giải pháp của cô là "một trong những công trình hay nhất trong lĩnh vực hình học đại số những năm gần đây."
Ngoài giải thưởng INSA, cô cũng đã được trao giải thưởng Ramanujan (2014), và Huy chương Saraswathi Cowsik (2013) do Hội cựu sinh viên Viện Nghiên cứu Cơ bản Tata (TIFR)
4. Thần đồng toán học giải được vấn đề 100 năm tuổi và từ chối giải thưởng 1 triệu USD

Giaỉ thuyết Poincare bắt nguồn từ một nhận xét có tính trực quan trong dân gian : Trong các “hình cầu – 2 chiều” thông thường, mọi đường cong khép kín đều có thể co lại liên tục thành một điểm trên mặt phẳng. Năm 1904 Poincare đặt lại vấn đề : liệu kết quả trên có còn đúng hay không đối vối một “Hình cầu – 3 chiều”? Bài toán Poincare này một định lý tưởng như không thể giải quyết được.
Tuy nhiên, nhà toán học Nga Grigory Perelman đã xuất bản chứng minh định lý vào năm 2002 và 2003, và theo The Utopianist, phải đến năm ngoái một đội ngũ các nhà toán học tại Viện Toán học Clay (CMI) đã chứng minh kết quả ông là chính xác.
Phần thưởng của ông ấy à? Một triệu đô la và huy chương Fields, giải thưởng tương đương với giải Nobel toán học. Nhưng Perelman lại miễn cưỡng chấp nhận tiền mặt, ông cho rằng rằng những kiến thức đã thu được từ chứng minh gải thuyết có giá trị hơn bất kỳ lợi nhuận nào mà nó đem lại.
5. Người phụ nữ giải quyết được “Bài toán Monty Hall” gây nên một cuộc tranh cãi dữ dội

Bài toán này thực sự rất thú vị, nhưng giải pháp của nó khiến mọi người phát điên. Và khi Marilyn vos Savant, một người phụ nữ biết đến vì có chỉ số IQ cao nhất được ghi nhận trong Sách kỷ lục Guinness, giải quyết nó, một số người không hề hài lòng.
Chúng ta đang nói về "Bài toán Monty Hall," trở nên nổi tiếng bởi chương trình trò chơi “Let’s make a deal”, được tổ chức bởi người dẫn chương trình đồng thời cũng là đồng sáng lập trò chơi tên là Monty Hall. Giả sử bạn là thí sinh tham dự chương trình. Có ba cửa ra vào, đằng sau một cánh cửa là một chiếc xe hơi, và phía sau hai cánh cửa kia là dê (có vẻ không liên quan lắm nhỉ). Người chơi chọn một cánh cửa, và sau đó trước khi nói ra thứ ở đằng sau cánh cửa đó, Hall mở ra một cánh cửa có con dê, để lại cửa người chơi chọn, và một cánh cửa còn lại không được mở. Câu hỏi đặt ra là người chơi có nên tahay đổi lựa chọn tăng cơ hội trúng được xe không?
Khi một độc giả gửi câu hỏi tới cột báo của Savant có tên Ask Marilyn, cô trả lời: "Có, bạn nên chuyển đổi." Nhưng câu trả lời của cô đã tạo ra một sự phản đối dữ dội. Cô nhận được hàng ngàn lá thư tuyên bố rằng cô đã sai, thậm chí một số thư thậm chí còn đi kèm với định kiến phân biệt giới tính như "Logic của phụ nữ không thể chấp nhận được" Tất cả điều này đã gây sốc cho Savant, chủ yếu là bởi vì vấn đề đã thực sự được giải quyết nhiều lần trước đây, như vào năm 1889 bởi nhà toán học người Pháp Joseph Bertrand. Cuối cùng Savant đã thuyết phục được nhiều độc giả của mình rằng cô đã đúng.
6. “Người máy tính” giải quyết được căn bậc 3 phức tạp khi chỉ mới lên 5 tuổi

Thần đồng tính toán Ấn Độ Shakuntala Devi đã giải quyết các vấn đề toán học phức tạp nhất một cách dễ dàng khiến mọi người phải thán phục trước khả năng của bà. Sinh ra ở Bangalore vào ngày 04 Tháng 11 năm 1929, khi bà mới chỉ 5 tuổi, khi, không giống như những đứa trẻ khác vẫn đang tập đếm, bà đi cùng với cha của mình và giải quyết các bài toán căn bậc 3 phức tạp trong các buổi diễn để kiếm tiền cho gia đình.
Devi lớn lên và trở thành không chỉ là một phù thuỷ toán học đi khắp thế giới đem lại cho nó cái nhìn thoáng qua của phi thường, mà còn là một người phụ nữ được mệnh danh "máy tính con người" của thế giới. Những kì công tuyệt với của bà đã đượcghi lại trong ấn bản năm 1982 của Sách kỷ lục Guinness World Records. Một số trong những tài năng số học của bà khiến thế giới không khỏi kinh ngạc:
• Bà có thể cộng 4 số phức tạp và nhân kết quả với 9878 trong 20 giây.
• Bà có thể khai căn bậc 23 của một số có 201 chữ số trong 50 giây
• Bà có thể nhân 2 con số 13 chữ số: 7.686.369.774.870 và 2.465.099.745.779 chỉ trong 28 giây, kết quả là 18,947,668,177,995,426,462,773,730. Thực sự là rất đáng ngưỡng mộ phải không?
7. Nhà toán học Anh giành được giải thưởng 720.000 USD nhờ giải được định lý 300 năm tuổi

Năm 1993, Andrew Wiles đã giao kết quả nghiên cứu bảy năm của mình về “Định lý cuối cùng của Fermat” cho Đại học Cambridge. Khi nhà toán học người Anh viết chứng minh của ông trên bảng đen ở phần cuối của bài trình bày của mình, 200 nhà nghiên cứu tham dự các bài giảng ngồi trong im lặng sững sờ và khen ngợi phần trình bày của ông.
Nghiên cứu của Wales có sự thay đổi rõ rệt đặc biệt là khi một lỗi đã được ghi nhận vào năm 1994, nhưng công sức 20 năm nghiên cứu của ông đã được đền đáp xứng đáng khi ông đã được trao giải Abel rất có uy tín của Viện Hàn lâm Khoa học và Văn chương Na Uy ở thủ đô Oslo. Giải thưởng này thường được gọi là giải Nobel của toán học đi kèm với 6 triệu kroner Na Uy (720.000 USD) tiền thưởng.
Pierre de Fermat đã đề xuất định lý cuối cùng của ông năm 1637, trong đó nêu "an bn = cn. Phương trình này không có nghiệm với số nguyên n≥3." Nói cách khác, phương trình có nghiệm với n không lớn hơn 2. Nhìn có thể có vẻ đơn giản, nhưng định lý này đã ám ảnh các nhà toán học suốt nhiều thế kỷ. Dưới đây là video giải thích rõ hơn về vấn đề này:
8. Học sinh người Ấn Độ giải được bài toán 350 tuổi của Newton

Năm 2012, một học sinh Ấn Độ 16 tuổi đang sống ở Đức tìm cách giải câu đố mà làm giới toán học đâu đầu trong suốt hơn 350 năm. Shouryya Ray, từ Dresden, đã được ca ngợi là một thiên tài sau khi giải được vấn đề đặt ra bởi Isaac Newton.
Ray đã giải quyết được hai lý thuyết động lực hạt cơ bản mà trước đây các nhà vật lý chỉ có thể tính toán bằng cách sử dụng siêu máy tính. Giải pháp của cậu có nghĩa là các nhà khoa học có thể tính toán đường bay của một quả bóng ném và sau đó dự đoán nó sẽ va chạm và bật lại tường như thế nào.
Ray tình cờ gải quyết được vấn đề trong một bài giảng tại Đại học Dresden. Giáo sư tuyên bố chúng không thể giải được, nhưng Ray đã quyết định thử sức. "Tôi chỉ tự hỏi," Tại sao không? "
9. Học sinh người Nigeria giải được vấn đề toán học mang tính lịch sử ngay học kì đầu ở đại học

Một sinh viên người Nigeria đạt được điểm số cao nhất tại một trường đại học ở Nhật Bản trong 50 năm qua và đã giải quyết vấn đề toán học trong học kỳ đầu tiên của mình mà tưởng như không thể giải quyết được trong hơn 30 năm.
Ufot Ekong, từng theo học tại Đại học Tokai ở Tokyo, đã đạt được bằng xuất sắc ngành kỹ thuật điện và đạt điểm cao nhất tại trường từ năm 1965. Trong suốt sự nghiệp đại học của mình, Ekong đã giành sáu giải thưởng học tập xuất sắc. Nhà toán học này cũng đã làm việc hai công việc trong thời gian học để chi trả học phí.
Tham khảo: oddee.com
NỔI BẬT TRANG CHỦ
-

Nếu có trong tay tấm vải phát nhạc này của Nhật Bản, bạn sẽ may thứ gì?
Theo mô tả của startup, tiếng của "tấm" loa sẽ tương đương máy hút bụi trong nhà.
-

Điện thoại Android mini hãng lạ chỉ 4 inch, thiết kế đẹp, cấu hình khá, pin 3000mAh dùng thoải mái 2 ngày, ở Việt Nam giá tầm 3 triệu
